Archivo original, lo descargamos más abajo
Profesores: Casares, Virginia – Doulay, Victor
Correo: mvcasares23@gmail.com – bulavhd@gmail.com
Actividad 4: Número Enteros.
EL CONJUNTO DE LOS NÚMEROS ENTEROS
Llamamos ℕ al conjunto de los números naturales {1;2;3;4;5…}. Al anteponer un signo “-“ a cada uno de ellos, obtenemos sus opuestos. De esta manera, puede hallarse pares de números opuestos entre sí. Por ejemplo: -1 y 1, 5 y-5, -7 y 7, -42 y 42.
El número 0 es opuesto de sí mismo.
El conjunto de los números enteros está formado por los naturales, todos sus opuestos y el 0. Este conjunto se simboliza con la letra ℤ. ℤ={…;−3;−2;−1;0;1;2;3;…}
Muchos hechos que se presentan en la vida diaria pueden interpretarse con números positivos y números negativos, haciéndoles corresponder a determinadas expresiones los signos + y – respectivamente. Veamos algunos ejemplos:
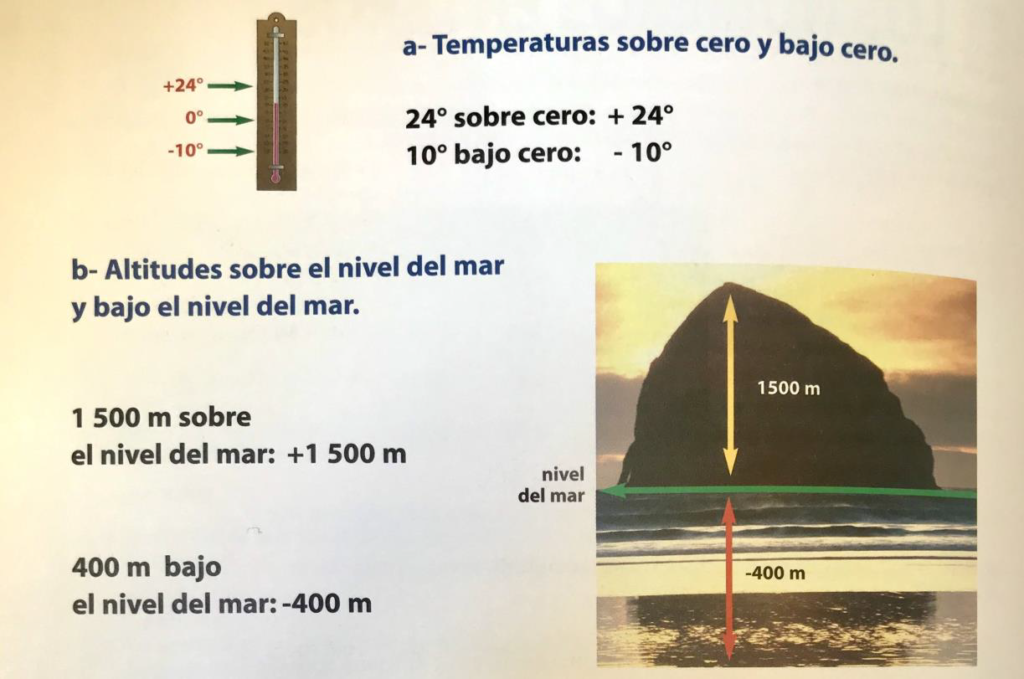
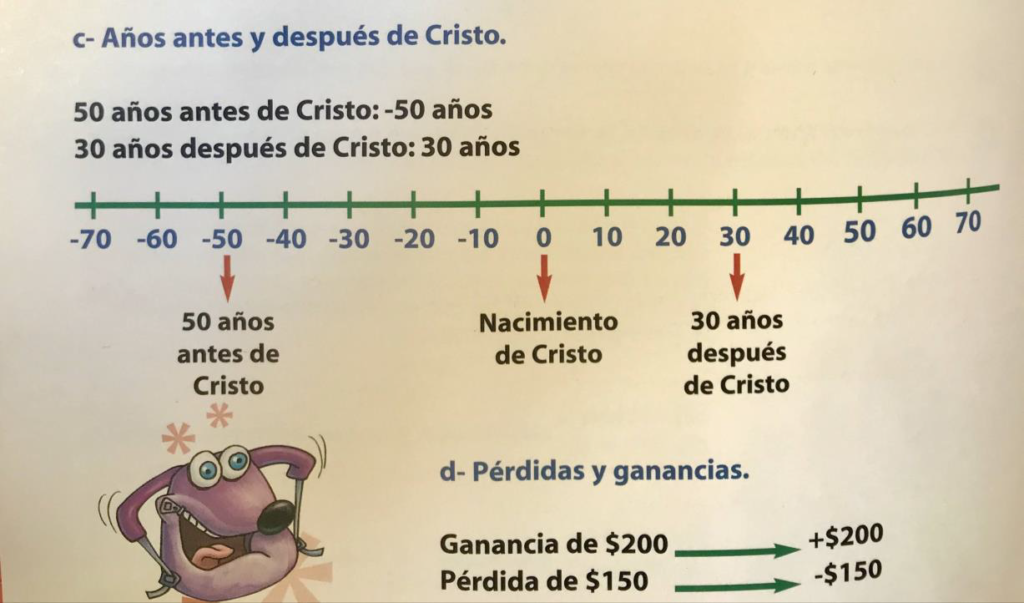
UBICACIÓN DE LOS NÚMEROS ENTEROS EN LA RECTA NUMÉRICA
Ya conocemos la recta numérica en la que se representan los números naturales, ahora incluyendo el cero, vamos a representar los números negativos.
- Dibujamos una recta.
- Señalamos el origen, que es el valor cero 0.
- Dividimos la recta en segmentos iguales (unidades), a la derecha e izquierda del cero.
- A la derecha del origen colocamos los números enteros positivos.
- A la izquierda del origen colocamos los números enteros negativos.
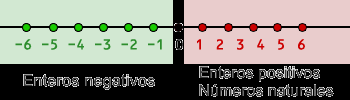
En la siguiente imagen podemos observar una recta numérica, donde se han ubicado números enteros. Si recorremos la recta de izquierda a derecha encontramos ubicado en primer lugar al número negativo menos seis, luego el menos cinco y sucesivamente así llegamos hasta el origen con valor 0. Luego continúan los números positivos, comenzando por el uno y terminando con el seis.
Ejemplo:
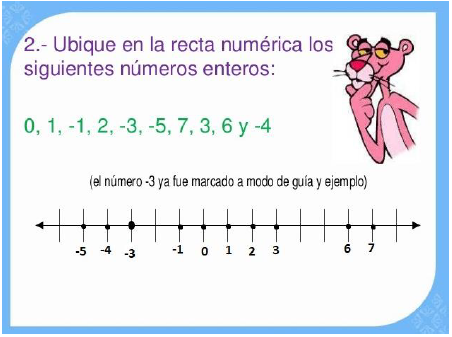
ORDEN DE LOS NÚMEROS ENTEROS
Ordenar números enteros a partir de su representación en la recta numérica:
Entre dos números enteros, es mayor el que más a la derecha está en la recta numérica
Entre dos números enteros, es menor el que más a la izquierda está en la recta numérica
Ordenar números enteros según su signo y valor absoluto:
Si dos enteros son positivos, el mayor es el que tiene mayor valor absoluto.
Por ejemplo: + 20 > +8
Cualquier número positivo es mayor que el cero, y el cero es mayor que cualquier negativo.
Por ejemplo: +8 >0 > -8
Entre dos números enteros negativos, es mayor el número que sin considerar el signo, representa una cantidad mayor que la otra. También se dice que un número negativo es mayor que otro cuando este está más cerca al 0, según la recta numérica o es menor que otro cuando este se aleja del 0, según la recta numérica.
Por ejemplo: -8 > –20
Actividad:
- Asocien un número a cada enunciado.
a) Tengo $20 en el bolsillo.
b) Debo $15 a un amigo.
c) El garaje está en el tercer subsuelo.
d) Yo vivo en el cuarto piso de un edificio.
e) Hace calor, el termómetro marca treinta y dos grados.
f) Hace frío, el termómetro marca cinco grados bajo cero.
g) La temperatura subió cuatro grados.
h) La temperatura bajó dos grados.
i) Gané $10.
j) Perdí $25.
k) El hecho ocurrió en el año 75 a.C.
l) Deposité un chuque de $30 en mi cuenta. - Ubiquen en la recta numérica los siguientes números enteros: 5; -8; -2; 3; -5; -7.
- Ordenen de menor a mayor estos números enteros: -4; -2; 20; -14; 10; -50; -8; 0; 3; 15.
- Completen con <? >.
a) -10______-20
b) 0_______-15
c) -21______21
d) -120_____120
e) -3______15
f) 25______79
g) -16______-105
h) -88______-89
i) 56______55
j) -110______-55
![]()
